在量子力学领域，有一个概念很容易被人误解，那就是 “测不准原理”，人们往往会觉得是因为我们的测量手段或方法存在问题才导致测不准。

但实际上，更为严谨科学的叫法应该是 “不确定性原理”。

“不确定性原理” 是由海森堡提出的，它并不是由于测量方式或测量仪器的问题导致的，而是量子世界所固有的一种属性，是量子世界的内在本质特征。

也就是说，量子世界的一切从根本上就是不确定的，无论我们使用多么精确先进的测量仪器，结果都是如此，这与测量方式方法毫无关系

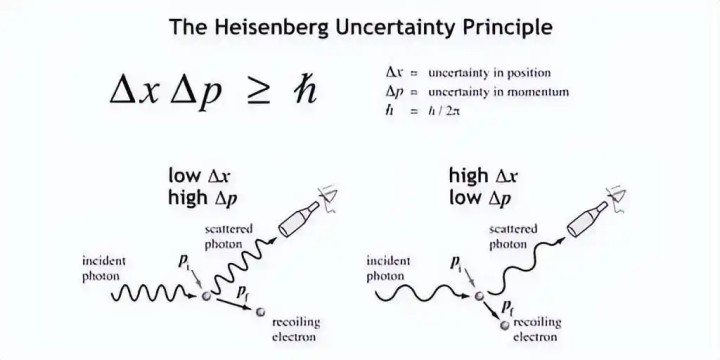
不确定性原理可以用公式 ΔxΔp≥h/4π 来表达。那么该如何理解这个公式呢？其实并不复杂，其中 Δx 表示位置的不确定性（即变化值），Δp 表示动量（也可以理解为速度）的不确定性，h 是普朗克常数，π 就是我们熟知的圆周率。

在量子力学中，我们常常会听到这样的观点：无法同时确定微观粒子的位置和速度。这其实从上述公式中就能体现出来。

因为位置不确定性与速度不确定性的乘积必须大于等于一个大于零的常数，虽然普朗克常数 h 非常小，但始终是大于零的。这就意味着位置的不确定性与速度的不确定性两者都不能为零，否则公式就不成立了。而不确定性不能为零，也就表明微观粒子本身就具有不确定性。

实际上，这个公式在宏观世界同样是成立的。只不过在宏观世界中，物体的质量相比于微观粒子要大得多，所以 Δx 与 Δp 通常都会很大，这样无论如何公式都是成立的，只是这种不确定性在宏观世界中表现得并不明显。

除了位置与速度存在这种不确定性关系之外，能量与时间也有类似的关系，用公式表示为 ΔEΔt≥h/4π，其中 ΔE 代表能量的不确定性（即变化值），Δt 代表时间的不确定性。

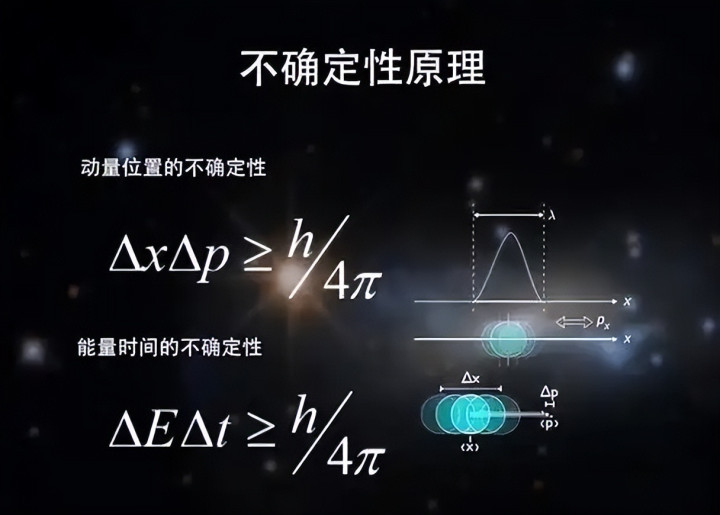
其实，能量与时间的这种不确定性关系，才是量子力学中最大的奥秘所在。量子世界里有许多诡异的现象，比如量子隧穿效应和量子涨落现象等，都可以通过能量与时间的这种不确定性关系来推导和解释。

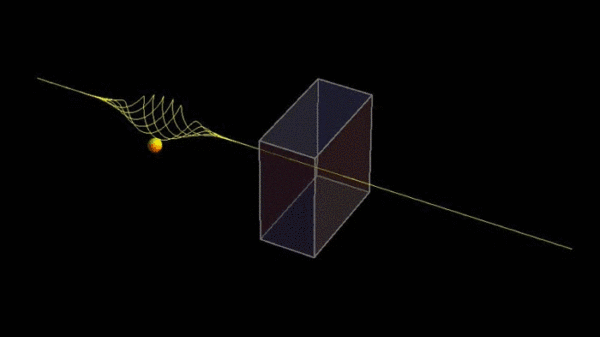
简单来说，当 Δt 足够小的时候，ΔE 可以变得非常大。这意味着在极短的时间内，能量的变化值能够变得极大。这就是为什么微观粒子有一定的几率可以穿越能量势垒的限制，能够瞬间穿越我们通常认为不可能跨越的势垒，实现量子隧穿。

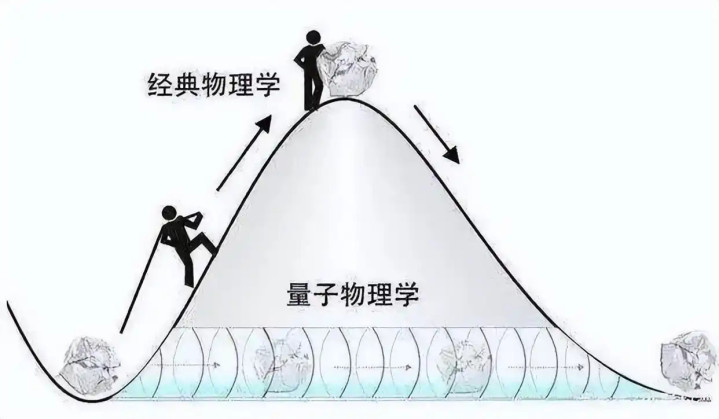
如果用宏观世界的现象来类比理解量子隧穿，就好比你要翻过一座山，正常情况下，你必须从山脚爬到山顶，然后再下到山的另一边，这个过程中你需要消耗一定的能量来克服 “能量势垒”，只有当你拥有的能量达到或者超过这个 “势垒” 时，你才能成功翻过这座山。

但是按照量子力学的思维方式，在足够短的时间内，你是有一定几率可以瞬间出现在山的另一边的，而不需要真的爬到山顶。就好像在现实世界中，有一堵 10 米高的墙，以我们的常规能力无论如何都无法翻越过去，但只要时间足够短，根据量子力学，你就有一定的几率可以直接穿过这堵墙。

从本质上讲，在时间足够短的情况下，很多看似不可能的事情都有发生的可能性，而且从量子力学的角度来看，最终一定会发生。

理解了这一点，真空中的量子涨落现象就比较容易理解了。在极短的时间内，虚粒子对可以凭空出现，然后又会瞬间湮灭并归还能量，这个过程并不违反能量守恒定律。

量子涨落现象对于我们理解宇宙大爆炸时的 “无中生有” 有着重要的意义。当 Δt 足够小（即时间变化足够小）的时候，ΔE（能量变化）就可以变得无限大，从理论上来说，甚至可以达到引发宇宙大爆炸所需的能量。

当然，这种情况发生的几率是非常小的，而且可能需要极其漫长的时间才有可能出现一次。但依据量子力学的诠释，任何只要有发生可能性的事情，最终都必然会发生。而在宇宙大爆炸之前，时间是不存在的，在这样的特殊条件下，宇宙大爆炸的发生也就成为了一种必然。